Eficiencia del generador
Para obtener buenos resultados de la simulación, es importante introducir los parámetros correctos. Cuando se trata de la entrada de corriente, tensión o potencia (dependiendo del tipo de sistema), es importante entender cómo se miden estos parámetros en la vida real y qué se puede utilizar como entrada para la simulación. En este artículo, veremos tres formas utilizadas para calcular o medir la potencia real en el inductor.
Adaptación de impedancias
Una de las razones por las que la potencia en la bobina es menor que en el generador son los diferentes valores de impedancia de la carga (bobina) y la fuente (generador). La impedancia se calcula como
donde - inductancia, - capacitancia, - resistencia, - frecuencia, - reactancia inductiva, - reactancia capacitiva.
El teorema de la máxima transferencia de potencia dice que para transferir la máxima cantidad de potencia de una fuente a una carga, la impedancia de la carga debe coincidir con la impedancia de la fuente.
Encontrar la potencia en el generador mediante simulación
La simulación puede utilizarse para estimar la eficiencia del sistema. Para utilizar la simulación, es necesario tener resultados conocidos del experimento, por ejemplo, la temperatura en la superficie de la pieza de trabajo o el perfil endurecido de la pieza. Estos resultados se utilizarán como referencia para saber si los parámetros de entrada en el inductor son correctos.
En primer lugar, realizará una simulación con los parámetros que se indican en el generador. Si la eficiencia real del sistema no es perfecta, verá que los resultados de la simulación dan valores de temperatura más altos para su pieza de trabajo, o un perfil templado demasiado ancho o profundo. Dado que la potencia en la simulación estará sobreestimada en comparación con la realidad, el siguiente paso es ajustar la potencia para obtener la temperatura que coincida con los resultados experimentales.
Importante: el valor de la potencia en la simulación sólo puede ser inferior a la potencia en el generador.
Cuando se encuentra el valor de potencia que da los resultados correctos, se puede calcular la eficiencia del sistema generador-inductor como:
Comparar la corriente en el generador con la corriente en la bobina
Para medir la corriente en la bobina tendrá que utilizar la bobina de Rogowsky. La bobina de Rogowsky debe ser adecuada para los parámetros de su sistema, como la corriente utilizada y el rango de frecuencia, se pueden encontrar fácilmente en muchas tiendas de Internet. La bobina de Rogowski es un dispositivo que funciona según el principio de que cuando se coloca alrededor del inductor, el campo magnético del inductor inducirá un voltaje en la bobina y el convertidor calculará la corriente en su inductor real. Ahora, al configurar la simulación, puede utilizar el valor de corriente medido en el inductor.
Casos controlados por voltaje
Si se utiliza un generador controlado por voltaje, significa que la tensión del generador se aplica conjuntamente a todo el sistema. Todo el sistema es un inductor junto con cualquier tipo de barras colectoras que lo conecten al generador.
Veamos un ejemplo muy sencillo: un circuito con dos componentes: generador y bobina. El generador da una tensión constante de 10 kV. La bobina tiene su inductancia L y su impedancia Z. Esto significa que la tensión es constante en todo el sistema, pero no en la bobina. Podemos imaginarnos todo el sistema como un circuito que consta de tres partes: barra colectora1 + inductor + barra colectora2. Como cada barra tiene su propia resistencia y , el circuito se puede redibujar para incluirlas.
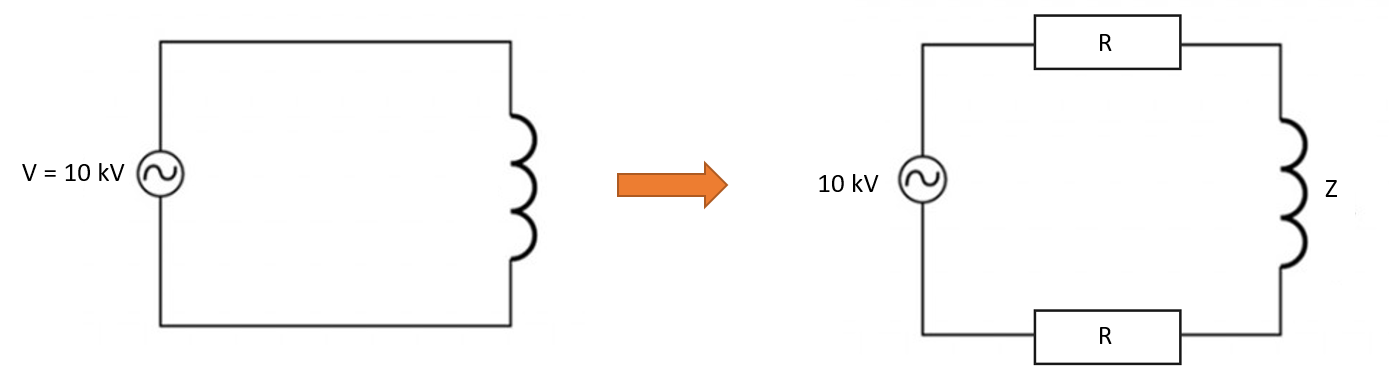
La resistencia de cada barra colectora puede calcularse
donde es la resistividad , l - longitud de la barra colectora, A - área donde fluye la corriente. Para calcular el área A, es necesario encontrar la profundidad (skin depth) en la que la corriente está fluyendo y calcular esta área. Por ejemplo, si el inductor es rectangular con longitudes laterales a y b, entonces el área A es
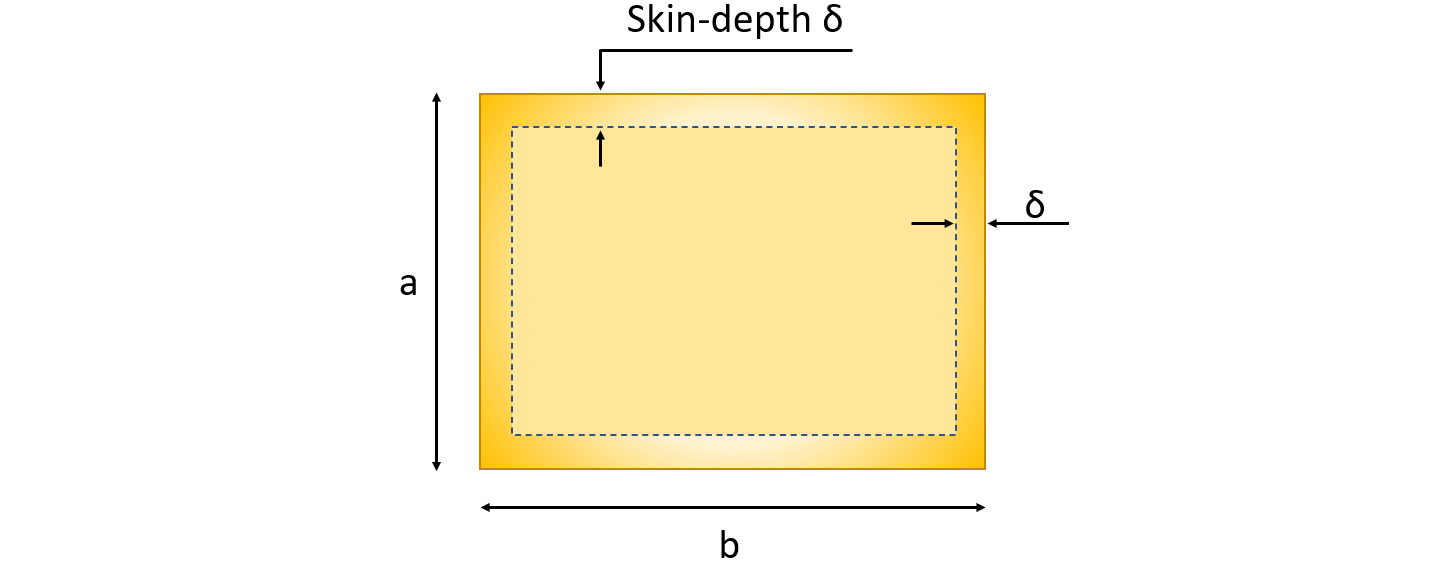
Cada parte - barras colectoras e inductor tiene su propia resistencia. Para las barras es constante, pero para la parte del inductor, tenemos que tener en cuenta su impedancia, que está cambiando en el tiempo debido al cambio de la permeabilidad magnética de la pieza de trabajo. Si nos fijamos en la resistencia total de tal circuito no es constante. Esto significa que la corriente tampoco es constante durante todo el proceso de calentamiento.
De aquí vemos que como la relación entre las resistencias no es la misma todo el tiempo, la caída de tensión en cada parte tampoco es constante en el tiempo. La relación de caída de tensión en las tres partes es la misma que para la resistencia .
Al hacer la simulación es importante tener en cuenta que la caída de tensión suele conocerse en todo el sistema, no en el inductor. La solución a este problema es hacer un corte en la geometría del inductor donde se aplica una condición de contorno de resistencia eléctrica. Para calcular la resistencia.
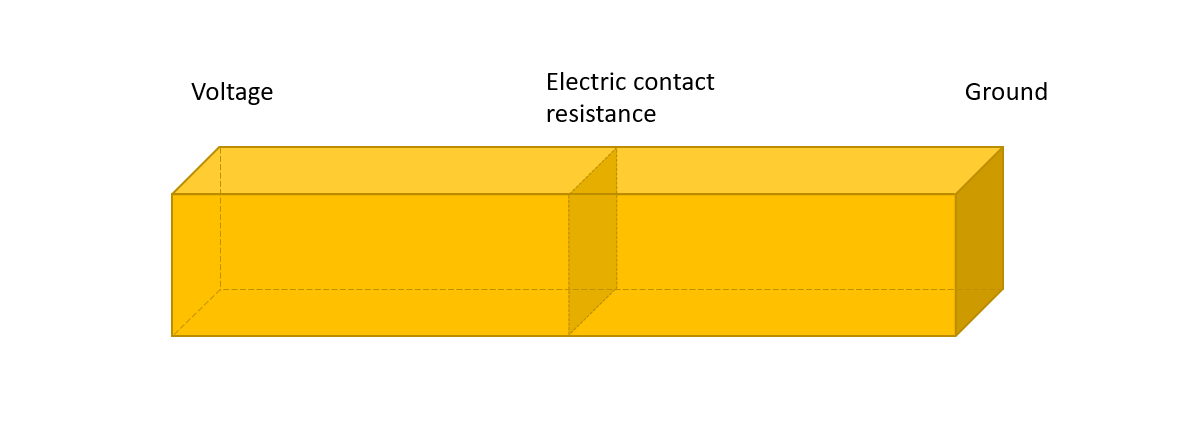
Para calcular la resistencia constante eléctrica, es necesario medir la longitud de las barras colectoras que quedan fuera de la geometría de simulación. Digamos que hay dos barras colectoras con una longitud de 1,2 m, la frecuencia utilizada es de 10 kHz, la sección transversal de la barra colectora es rectangular con longitudes laterales a = 10 cm, b = 12 cm. La profundidad de la piel en este caso es de 652 um. Para calcular el área por donde circula la corriente se utiliza la ecuación:
La resistencia de las barras colectoras es:
Ahora, para calcular la resistencia de contacto eléctrico, que tiene unidades , hay que multiplicar la resistencia total calculada de las barras colectoras por el área de la sección transversal del inductor:
Ahora, este valor representará toda la resistencia que no está incluida en el modelo de simulación pero sí en el sistema real.