Thermal shock

For results showing thermal shock (in the temperature scale you will notice a negative temperature), it is usually caused by either a huge time step, a too coarse mesh, or a combination of bot;, it mainly occurs in cases with very rapid heating or very high translational speed, we recommend you refine the mesh or/and reduce your time step.

What is thermal shock?

When an initially hot body is suddenly cooled or a cold body is suddenly heated through the surface, a steep variation in temperature called thermal shock may appear. An example of this might be heating with radiative heaters with known power or with resistive heaters mounted directly on the wall. In these cases one should use Heat flux $W/m^2$ or Heat flow $W$ boundary condition.

Thermal shocks have short-term effect and their effect vanishes when the temperature profile is developed. But proper resolution of these effects puts additional constraints on the time step and mesh resolution in FEM analysis:

$$\Delta t = \frac{\rho c}{\lambda} \frac{\Delta x}{6}$$

Here $\Delta t$ is the time step, $\Delta x$ is the mesh size. The coefficient 6 is empyrical, and varies in different literature sources.

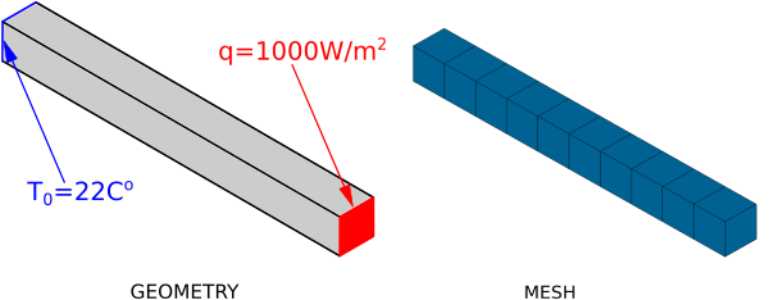
To illustrate the problem, let's consider 1D example (in CENOS it is made as 3D case with 1 element thickness in Y and Z directions and N divisions in X direction):

The bar has properties $\lambda = 50 W/mK$, $\rho = 1000 kg/m^3$, $c = 500 J/kg K$. The length is 1 m, initial temperature and temperature on the left side $T_0 = 22 C$, the heat flux $q = 1000 W/m^2$.

Let's consider the mesh with N = 5, so $\Delta x = 0.2 m$. This leads to the critical value of time step $\Delta t = 400 s$.

The temperature distribution in the bar after 50 seconds obtained with $\Delta t = 5$ and different mesh sizes are shown in the figure below:

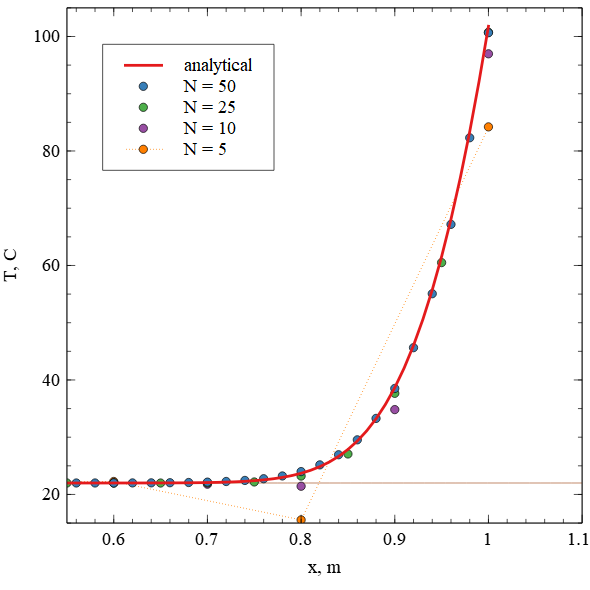
This figure shows that for the mesh with $N=5$ $(\Delta x = 0.2)$ unphysical temperature appears at the value $x=0.8$. Since initial condition and boundary condition on one end is 22 C, temeperature should never be below this value. In other words, the temperature and the mesh size are linked and cannot be chosen totally independently.

note

for further reading: https://hal-mines-paristech.archives-ouvertes.fr/hal-00576032/document